
Закон пропорций определяет отношения частей целого одна к другой и к самому целому.
Человеку свойственно стремление познавать окружающий его мир, учиться у Природы, давать объяснение различным явлениям, обобщать, делать выводы и затем использовать полученные знания в своих целях. Поэтому вполне естественно, что попытки «проверить алгеброй гармонию» предпринимались человечеством еще с древнейших времен.
Каждое существо, созданное Природой, представляет собой нечто единое, целое, от которого ничего нельзя отнять, не нарушив гармонии. В то же время и прибавить ничего нельзя. Именно поэтому различные уродства и увечья так режут глаз и вызывают подсознательное отвращение - нарушение гармонии мгновенно отмечается мозгом.
Пропорции человеческого тела меняются в зависимости от пола и возраста, и эти особенности необходимо учитывать при изображении людей.
Еще в глубокой древности было обнаружено, что все явления в природе связаны между собой, что все пребывает в непрерывном движении, изменении и, будучи выражено числом, обнаруживает удивительные закономерности. В Древней Греции возник ряд учений о гармонии. Из них наиболее глубокий след в мировой культуре оставило пифагорейское учение. Последователи Пифагора представляли мир, вселенную, космос, природу и человека как единое целое, где все взаимосвязано и находится в гармонических отношениях. Гармония здесь выступает как начало порядка - упорядочивания хаоса. Гармония присуща природе и искусству.
Пифагорейцы и их последователи всему сущему в мире искали числовое выражение. Ими было обнаружено, что математические пропорции лежат в основе музыки (отношение длины струны к высоте тона, отношения между интервалами, соотношение звуков в аккордах, дающих гармоническое звучание). Пифагорейцы пытались математически обосновать идею единства мира, утверждали, что в основе мироздания лежат симметричные геометрические формы.
Пифагорейцы искали математическое обоснование красоте. Они исследовали пропорции человеческого тела и утвердили математический канон красоты, по которому скульптор Поликлет создал статую «Канон». Все классическое искусство Греции носит печать пифагорейского учения о пропорциях. Его влияние испытали на себе ученые средневековья, наука и искусство эпохи Возрождения, Нового времени вплоть до наших дней. Вслед за пифагорейцами средневековый ученый Августин назвал красоту «числовым равенством». Философ-схоласт Бонавентура писал: «Красоты и наслаждения нет без пропорциональности, пропорциональность же, прежде всего, существует в числах. Необходимо, чтобы все поддавалось счислению». Об использовании пропорции в искусстве Леонардо да Винчи писал в своем трактате о живописи: «Живописец воплощает в форме пропорции те же таящиеся в природе закономерности, которые в форме числового закона познает ученый».
Таким образом, пропорциональность, соразмерность частей целого является важнейшим условием гармонии целого и может быть выражена математически посредством пропорций.
Целое всегда состоит из частей, части разной величины находятся в определенных пропорциях по отношению как одна к другой, так и к целому. Из многих пропорций, которыми издавна пользовался человек, одна обладает уникальными свойствами - это так называемое «золотое сечение». Считается, что форма, в основе которой лежат пропорции золотого сечения, является наиболее гармоничной и привлекательной для человека.
Примерами практического использования «золотого сечения» с целью построения гармоничной композиции могут служить знаменитый храм Парфенон, египетские пирамиды, скульптуры Фидия, работы Леонардо да Винчи и Альбрехта Дюрера и даже знаменитые скрипки Антонио Страдивари.
Золотое сечение - это такое деление отрезка на две неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей. Другими словами, меньший отрезок так относится к большему, как больший ко всему, т.е. a/b = b/с или c/b = b/а (рис. 3.5 ).

Если длину всего отрезка принять равной 1, а большую его часть обозначить через X, то из условий золотого сечения получим: 1/Х = Х/(1 - X). Преобразовав и решив это уравнение, получим, что его положительный корень одновременно выражает длину отрезками значение величины φ, а его десятичное разложение имеет вид 1,61803398... Интересно, что 1/φ = 0,61803398... Число φ - единственное положительное число, которое переходит в обратное ему при вычитании единицы. Это число тесно связано с метрическими свойствами некоторых правильных многоугольников и многогранников (пятиугольника, десятиугольника, додекаэдра, икосаэдра), так как оно равно 2cos(π/5). Подобно числу π, φ можно представить в виде суммы бесконечного ряда многими способами.
С золотой пропорцией тесно связаны работы итальянского математика-монаха Леонардо из Пизы, известного под именем Фибоначчи. В его труде «Книга об абаке», опубликованном в 1202 году, была задача о кроликах, в которой подсчитывалось, сколько кроликов родится за год от одной пары. В результате был открыт ряд цифр, известный в науке как ряд Фибоначчи. Его особенность заключается в том, что каждый член данного ряда, начиная с третьего, равен сумме двух предыдущих: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и так до бесконечности (2 + 3 = 5, 3 + 5 = 8 и т.д.). При этом отношение чисел ряда по мере возрастания все больше приближается к отношению золотого сечения - 21/34 = 0,617, 34/55 = 0,618 и т.д. Математическая связь между золотым сечением и числами Фибоначчи состоит в том, что отношение соседних чисел Фибоначчи в пределе стремится к золотой пропорции.
Астроном И. Кеплер писал: «Устроена она (золотая пропорция) так, что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности»
Число φ выражает также отношение радиуса окружности к стороне правильного вписанного десятиугольника. Если расположить три «золотых» прямоугольника («золотыми» считаются такие прямоугольники, стороны которых относятся одна к другой в «золотом» соотношении, например 62 х 38) таким образом, чтобы каждый пересекался с двумя другими под прямым углом к каждому из них, можно заметить, что вершины «золотых» прямоугольников совпадают с 12 вершинами правильного икосаэдра и одновременно указывают расположение центров 12 граней правильного додекаэдра. Золотой прямоугольник обладает многими необычными свойствами. Если отрезать от него квадрат, сторона которого равна меньшей стороне прямоугольника, мы снова получим золотой прямоугольник меньших размеров. Продолжая отрезать квадраты, мы будем получать все меньшие и меньшие золотые прямоугольники. Причем располагаться они будут по логарифмической спирали, имеющей важное значение в математических моделях природных объектов (например, в раковинах улиток).
Считается, что впервые понятие золотой пропорции ввел в научный обиход древнегреческий философ и математик Пифагор (VI в. до н.э.). Есть предположение, что Пифагор, в свою очередь, позаимствовал его у египтян и вавилонян. Для этого имеются достаточно веские основания, так как пропорции пирамиды Хеопса, древнеегипетских храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют о том, что египетские мастера знали золотую пропорцию и умели ею пользоваться. Французский архитектор Ле Корбюзье обнаружил, что на рельефе из храма фараона Сети I в Абидосе и рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого сечения. Зодчий Хесира, изображенный на рельефе деревянной доски из его гробницы, держит в руках измерительные инструменты, в которых также зафиксированы пропорции золотого сечения (рис 3.6 )
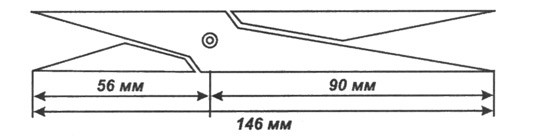
Рисунок 3.6
Изучая форму спирально закрученной раковины, Архимед вывел уравнение спирали, шаг которой равномерно увеличивается в пропорциях золотого сечения. Эта спираль получила название «спираль Архимеда» и нашла широкое применение в технике.
Логарифмическую («золотую») спираль можно построить двумя способами: по отрезкам восходящего ряда золотой пропорции и с помощью золотых прямоугольников (рис. 3.7).
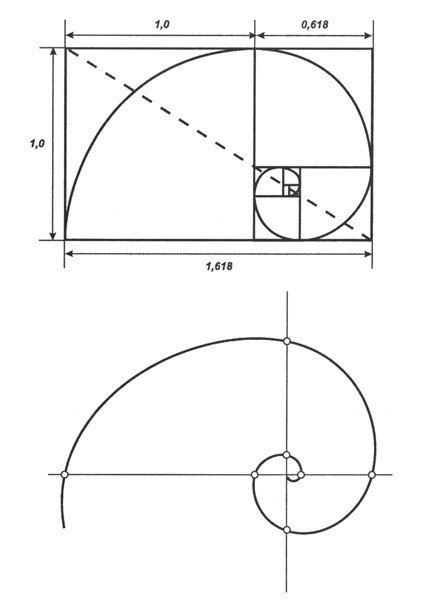
Рисунок 3.7
Изучал свойства логарифмической спирали и С.М. Эйзенштейн (1898-1948), который построил свой знаменитый фильм «Броненосец «Потемкин»« по золотому сечению.
Одной из причин, по которой пифагорейцы избрали пентаграмму (пятиконечную звезду, вершины которой соединены между собой отрезками) символом своего тайного ордена, является то обстоятельство, что любой отрезок в этой фигуре находится в золотом отношении к наименьшему соседнему отрезку. Каждый луч пятиконечной звезды представляет собой так называемый «золотой треугольник», стороны которого образуют угол 36° при вершине, а основание, отложенное на его боковую сторону, делит ее в золотой пропорции (рис 3.8 ).
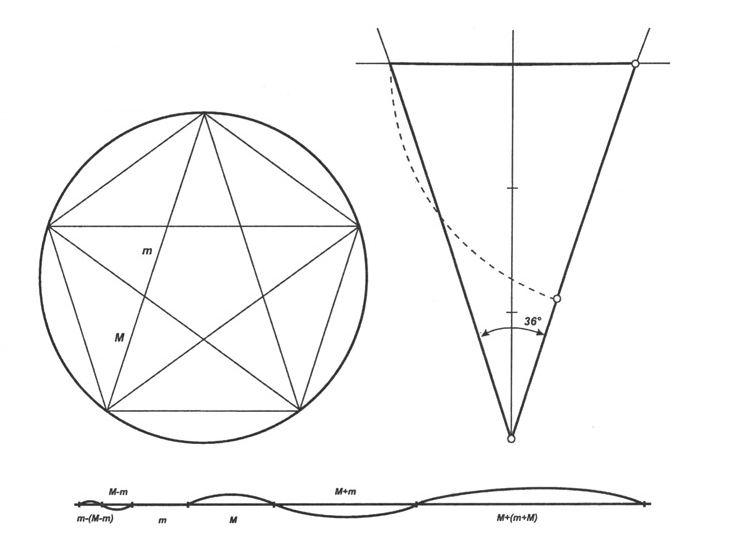
Рисунок 3.8
Пентаграмма играла важную роль во всех оккультных науках. Пятиконечная звезда, буквально пронизанная пропорциями золотого сечения, использовалась, как известно, и в коммунистической символике.
В средние века секреты золотой пропорции хранились в тайне, а пятиугольная пентаграмма Пифагора считалась демоническим символом. Однако в эпоху Возрождения интерес к золотому сечению усилился.
Большое внимание изучению золотых пропорций уделял великий Леонардо да Винчи. Именно он впервые назвал золотую пропорцию «золотым сечением», и это название используется по сей день. Леонардо даже начал писать книгу по геометрии, в которой собирался описать и золотое сечение, но не закончил ее, так как в это время (в 1509 году) появилась книга итальянского монаха-математика Луки Пачоли «Божественная пропорция». Книга была великолепно иллюстрирована, и существуют мнения, что это сделал Леонардо да Винчи. Лука Пачоли был учеником художника Пьеро делла Франчески, основателя начертательной геометрии и автора двух книг, одна из которых называлась «О перспективе в живописи». Будучи монахом, Лука Пачоли среди прочих достоинств золотого сечения приводил его «божественную суть» как выражение божественного триединства, имея в виду, что малый отрезок - олицетворение Бога-Сына, больший отрезок - Бога-Отца, а весь отрезок - Бога-Духа Святого.
В это же время в Германии золотой пропорцией занимался не менее известный художник Альбрехт Дюрер (1471-1528). Имеются свидетельства, что он встречался с Лукой Пачоли во время своего пребывания в Италии. Дюрер применял золотое сечение при измерениях человеческого тела.
Особенно популярным среди ученых и художников золотое сечение стало в середине XIX века. В 1855 году немецкий профессор Адольф Цейзинг опубликовал солидный (457 страниц) труд «Эстетические исследования», в котором доказывал, что из всех пропорций именно золотое сечение дает максимальный художественный эффект и доставляет наибольшее удовольствие при восприятии. Именно в золотом сечении, по Цейзингу, кроется ключ к пониманию всей морфологии (в том числе строения человеческого тела) искусства, архитектуры и даже музыки.
Цейзинг измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа - важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13:8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8:5 = 1,6. У новорожденного пропорция составляет отношение 1:1, к 13 годам она равна 1,6, а к 21 году равняется мужской.
Пропорции золотого сечения проявляются и в отношении других частей тела - длина плеча, предплечья и кисти, кисти и пальцев и т.д. (рис. 3.9).
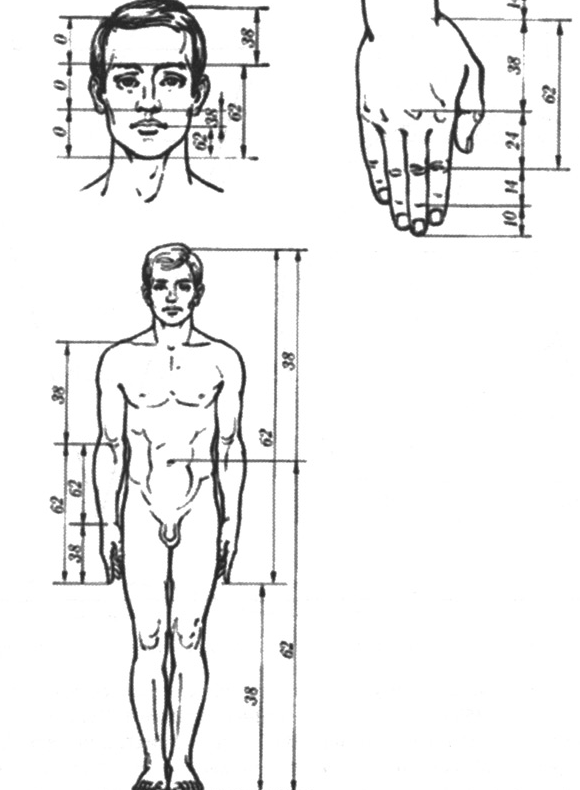
Рисунок 3.9
Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского.
Греческий скульптор Леохар создал знаменитую статую Аполлона Бельведерского, воплотившую представление древних греков о красоте. Если высоту статуи разделить в отношении золотого сечения и то же самое проделать с каждой частью, то точки деления придутся на талию, коленную чашечку и адамово яблоко. Та же закономерность распространяется в отдельности на лицо, руку и кисть.
Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры. Цейзинг дал определение золотому сечению, показал, как оно выражается в отрезках прямой и в цифрах. Когда цифры, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют ряд чисел Фибоначчи, который можно продолжать до бесконечности в одну и в другую сторону.
Другой немецкий ученый-физиолог, Густав Фехнер, пытался практически обосновать взгляды Цейзинга. Для этого он измерил отношения сторон у тысяч окон, картинных рам, игральных карт, книг и других прямоугольных предметов, проверил, в каком отношении поперечные перекладины могильных крестов на кладбищах делят вертикальные основания, и обнаружил, что в большинстве случаев полученные им числа мало отличаются от ср. Фехнер разработал целый ряд остроумных тестов, в которых испытуемому предлагалось выбрать «милый его сердцу» прямоугольник из большого набора прямоугольников с различными соотношениями сторон, нарисовать самый «приятный» многоугольник, выбрать место перекладины и т.д. И здесь многократно проведенные опыты показали, что испытуемые отдают предпочтение отношениям, близким к φ.
И в растительном, и в животном мире явственно прослеживается определенная ритмичность, симметрия относительно направления роста и движения. Сон и бодрствование человека в течение суток, расположение листьев на ветке, расположение семян подсолнечника, игл кактуса, энергетические переходы элементарных частиц, генные структуры живых организмов, биоритмы мозга и зрительное восприятие - везде проявляются закономерности золотой симметрии.
Таким образом, можно заключить, что несмотря на огромное разнообразие форм, существующих в природе, везде наблюдаются закономерность и система, основой которой служит золотая пропорция. В отличие от обычной симметрии, когда объект разделяется строго на две равные части, золотая пропорция является симметрией динамической, отражающей рост и движение.
Дизайнера, в первую очередь, интересует практический аспект применения золотого сечения. Золотое сечение активно использовалось в архитектуре и живописи, поэтому, для того чтобы лучше понять принципы золотого сечения, имеет смысл проанализировать известные произведения искусства.
Известно, что такие художники, как И.Е. Репин, Г.И. Семирадский, В.В. Стасов, К.А. Савицкий, знали и применяли в своих произведениях золотую пропорцию.
В Русской академии художеств был разработан упрощенный метод композиционного построения картин, согласно которому плоскость холста делилась на 10 частей по вертикали и по горизонтали. Линия золотого сечения в результате располагалась в отношении 6 и 4 частей, что давало пропорцию, близкую к золотому сечению (62:38), и позволяло ориентироваться и правильно располагать важные объекты.
Академик А.Н. Лаптев в статье «Некоторые вопросы композиции» писал: «Хочу упомянуть о давно известном, особенно в классическом искусстве, законе пропорций золотого сечения. В силу некоторого свойства нашего зрительного восприятия эти пропорции (примерно 6 и 4) являются наиболее гармоническими и наиболее отвечающими общему понятию красоты, а потому и наиболее часто употребимыми».
Тех же пропорций придерживались художники Мюнхенской академии путем деления картины на 5 частей. Золотая пропорция бралась при этом в отношении 3:2, что одно и то же, так как уменьшение чисел ряда 10, 6 и 4 в два раза дает 5, 4 и 2 (рис. 3.10).
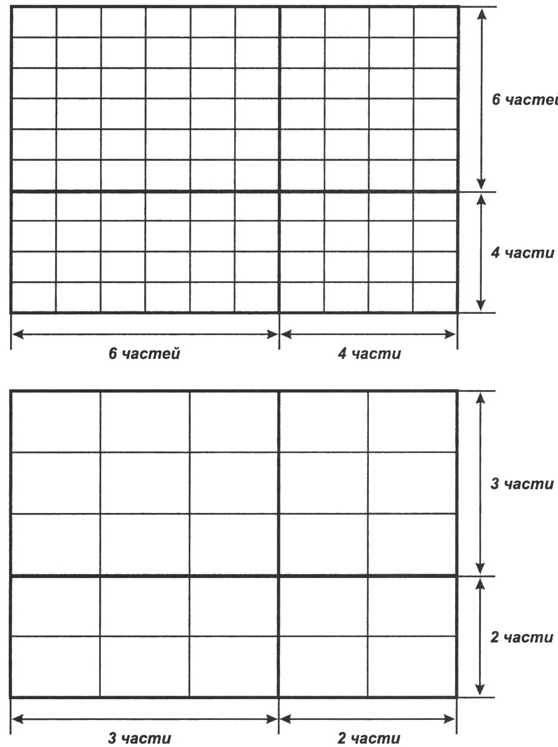
Рисунок 3.10
На практике нет необходимости заниматься сложными математическими расчетами - вполне достаточно знать основные числа золотого сечения: 62, 38, 24, 14 и 10. Этот ряд несложно продолжить (каждое последующее число равно сумме двух предыдущих). При использовании какого-либо пакета для работы с компьютерной графикой достаточно один раз построить отрезок длиной 100 мм и разделить его на части, равные 62 и 38 мм соответственно. После этого его можно масштабировать и вращать, используя в качестве пропорциональной линейки и выстраивая с его помощью модульный каркас макета (для этих целей могут быть также использованы направляющие, работу с которыми поддерживают все современные пакеты компьютерной графики).
Привыкнув делить композицию в соответствии с золотой пропорцией, можно без особого труда отыскать ее в самых разных произведениях (рис. 3.11).

Рисунок 3.11
Несмотря на свою гармоничность и универсальность, золотое сечение нельзя считать единственно верным принципом композиционных построений. Композиция, построенная по принципу золотого сечения, отличается сбалансированностью, спокойствием и цельностью, однако это не всегда то, что требуется дизайнеру. Во многих случаях (например, на рекламных плакатах), наоборот, требуется показать экспрессию, резкую динамику, создать агрессивный, подчас шокирующий образ. Да, золотое сечение можно считать классикой композиции, но не рецептом на все случаи жизни.